Entrando en términos profundos, la teoría matemática define la belleza matemática a través de 4 aproximaciones distintas: belleza en el método, belleza en la geometría, belleza en la experiencia y belleza en los resultados. En este último tipo de belleza matemática se encuentra la identidad de Euler, fórmula que hoy queremos destacar y que el premio nobel de física Richard Feynman calificó como «la fórmula más notable de la matemática».
¿Pero qué es lo que hace tan destacable esta fórmula? Es bella por su extraordinaria sencillez y porque resulta ideal para aprender matemáticas, pues se podría decir que estas aparecen resumidas en la fórmula casi por completo.
El autor de la ecuación matemática más famosa es Leonhard Euler, de ahí que lleve su nombre: la identidad de Euler, llamada «identidad» porque en ella solo existen números. Aunque en la fórmula veamos letras, estas representan en realidad números. Pero no se trata de números cualesquiera, sino de los más famosos de las matemáticas: el número pi, el número e (precisamente así llamado también por Euler), el número i, la unidad y el cero. En esta identidad encontramos también los conceptos de suma, multiplicación, exponenciación e identidad y los cinco números fundamentales.
Esta identidad se puede utilizar para obtener coordenadas con unos cálculos ridículos y una precisión asombrosa sin necesidad de calcular senos y cosenos… fue el primer paso (o uno de los primeros) para los sistemas GPS y GPRS que utilizan las coordenadas polares para determinar la posición del dispositivo y permitir su comunicación.
Y la belleza de todas estas cuestiones es la misma que pueda tener una obra de Shakespeare o un cuadro de Monet… con la diferencia de que la Identidad de Euler seguirá siendo cierta cuando todos los cuadros y libros se hayan quemado. “
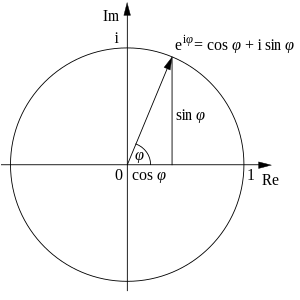
En términos trigonométricos, ya
no suena tan formidable, y quiere decir que el coseno de 180 grados es -1, (cos
180 = -1) y su representación gráfica es:

Comentarios
Publicar un comentario