Mecanismos (Biela_Manivela_Corredera)

El sistema funciona de la siguiente forma:

• El eje tiene un movimiento giratorio que transmite a la manivela.

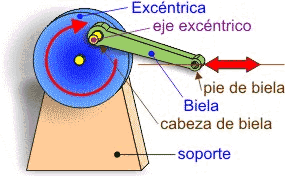
• La manivela (o la excéntrica) convierte el movimiento giratorio del eje en uno circular en su empuñadura (eje excéntrico).

• La cabeza de la biela está unida a la empuñadura de la manivela (eje excéntrico) y, por tanto, está dotada de un movimiento circular.

• En su movimiento circular, la cabeza de la biela arrastra el pie de biela, que sigue un movimiento lineal alternativo.

La trayectoria seguida por el pie de biela es lineal alternativa, pero la orientación del cuerpo de la biela cambia en todo momento. 

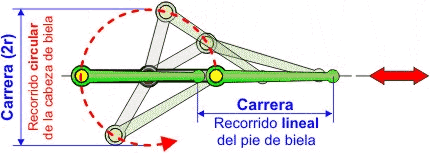
• La longitud del brazo de la manivela determina el movimiento del pie de la biela (carrera), por tanto, hemos de diseñar la manivela con longitud mucho más corta que la biela.

Carrera=2 veces el radio de la manivela

• Para que el sistema funcione adecuadamente se se deben emplear bielas cuya longitud sea, al menos, 4 veces el radio de giro de la manivela a la que está acoplada.
• Cuando tenemos que transformar movimiento giratorio en alternativo, el eje de la manivela es el elemento motriz y el pie de biela se conecta al elemento resistente (potencia útil). Esto hace que la fuerza aplicada al eje se reduzca en proporción inversa a la longitud de la manivela, por lo que cuanto mayor sea la manivela menor será la fuerza que aparece en su empuñadura y consecuentemente en el pie de la biela.
• Las cabezas de las bielas deben de estar centradas en la empuñadura sobre la que giran, por lo que puede ser necesario aumentar su anchura (colocación de un casquillo).

Referencias: 

[1] "Mecanismo biela-manivela". IES MARE NOSTRUM – Instituto de Enseñanza Secundaria y Formación Profesional IES Mare Nostrum, Alicante. https://www.iesmarenostrum.com/departamentos/tecnologia/mecaneso/mecanica_basica/mecanismos/mec_biela-manivela.htm (accedido el 5 de febrero de 2023).